2  Quantum Ising systems

Magnetism and magnetic interactions and ordering will be a common feature of all the systems we describe. Electron spin is the origin of all magnetism and the magnetic properties of any material are determined by the distribution of unpaired electron spins within the material. A common approach to studying quantum phase transitions is to determine the lowest-energy or "ground" state of the material at zero temperature and a fixed value of some variable such as pressure. It is also important to know the low-energy excitations of the system. It is often found that the ground state will be different at a different value of the relevant variable. This means that the material must undergo a phase transition as this variable is changed - even at absolute zero. This is the quantum phase transition.

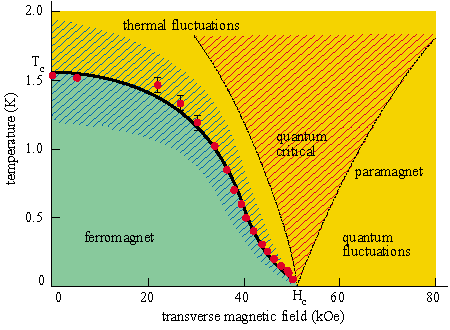
	Figure 1: Quantum criticality in a ferromagnet.
	The temperature-magnetic field phase diagram of LiHoF4 as measured by Bitko and co-workers. The full black line is a line of phase transitions separating the ferromagnet (green) and the paramagnet (yellow). A classical phase transition takes place at H = 0, T = Tc and a quantum phase transition occurs at the point H = Hc, T = 0. An effective classical theory applies within the blue hatched region, while the influence of the quantum critical point is predominant in the red hatched region. Bitko and co-workers used measurements of magnetic susceptibility to determine the different Curie points (red circles).

Consider the ionic crystal lithium holmium fluoride (LiHoF₄). The magnetic properties of this rare-earth insulator are well understood on the microscopic scale. In particular, at temperatures below about 2 K, the only important magnetic excitations reside on the holmium ions (which have a charge of +3) and the spins on neighbouring ions are coupled by the magnetic dipolar interaction. These spins can either point "up" or "down" relative to a certain crystalline axis. Such an arrangement of spins on a lattice is known as an Ising model. The geometry of the crystal is such that, in the absence of an external magnetic field, the lowest energy state is very simple: either all the spins point up or they all point down. In other words, LiHoF₄ is a fully polarized ferromagnet.

In 1996 David Bitko and Thomas Rosenbaum of the University of Chicago, and Gabriel Aeppli of NEC Research in Princeton investigated the behaviour of LiHoF₄ as a function of temperature, T, and an external magnetic field. First, consider the case of no magnetic field (the y-axis in Fig 1). Initially thermal fluctuations caused a small number of spins to flip: that is, if the crystal was in a ground state with all the spins pointing up, thermal fluctuations caused some spins to point down, and vice versa. As the temperature was increased, the number of minority spins also increased until there was an equal number of up and down spins. This was a conventional, second-order phase transition, driven entirely by thermal fluctuations, from a ferromagnetic state to a paramagnetic state at the Curie temperature.

The novel property of LiHoF₄ is that it is possible to destroy the ferromagnetic order by turning an entirely different knob, even at absolute zero. An external magnetic field, H, applied at right angles to the Ising spin orientation, allows quantum tunnelling to take place between the up and down spin states. If this field is larger than a critical field, H_c, these tunnelling events are frequent enough that ground state becomes a paramagnet, even at zero temperature. In other words, a phase transition driven entirely by quantum fluctuations has occurred.

However, unlike the earlier thermal transition, it is now quite misleading to think of the paramagnetic state as having spins which are fluctuating between the up and down states in real time; rather there is a unique phase-coherent wavefunction for the ground state that is a quantum superposition of the up and down states. The properties of this quantum paramagnet are well understood.

So what happens in the remainder of the phase diagram, when both H and T are non-zero? The classical phase transitions at zero field and the quantum phase transition at zero temperature are connected by a line of second-order phase transitions which separates the ferromagnet from the paramagnet. The dynamic properties of the thermal paramagnet are quite distinct from those of the quantum paramagnet, but these two regions of the phase diagram are nevertheless continuously connected without any intervening thermodynamic singularity. Instead there is a smooth crossover through an intermediate "quantum critical" region (Fig 1). In a sense, quantum and thermal fluctuations are equally important in this region, and conventional models do not apply here. Developing the correct theoretical framework to explain the behaviour observed in this regime has been an important focus of recent research. In particular, as we will discuss more explicitly for the examples that follow, many macroscopic properties are determined only by the the temperature and the values of fundamental physical constants, like the electron magnetic moment and the electron charge. Put another way, the macroscopic properties of the quantum critical regime are often independent of microscopic details.

Some readers will be aware that strong fluctuations in the vicinity of a second-order phase transitions lead to a divergence in the magnetic susceptibility, and that this divergence is characterized by a "critical" exponent that is independent of the material properties. In fact, the critical divergence observed near the classical transition at zero field also applies sufficiently close to the entire phase boundary, with the exception of the quantum critical point itself at absolute zero (Fig 1). This means that classical behaviour can always be observed sufficiently close to the phase boundary. Indeed, the quantum critical region is actually farther away from the phase boundary that this classical region, except at the quantum critical point.