4  Spins and stripes

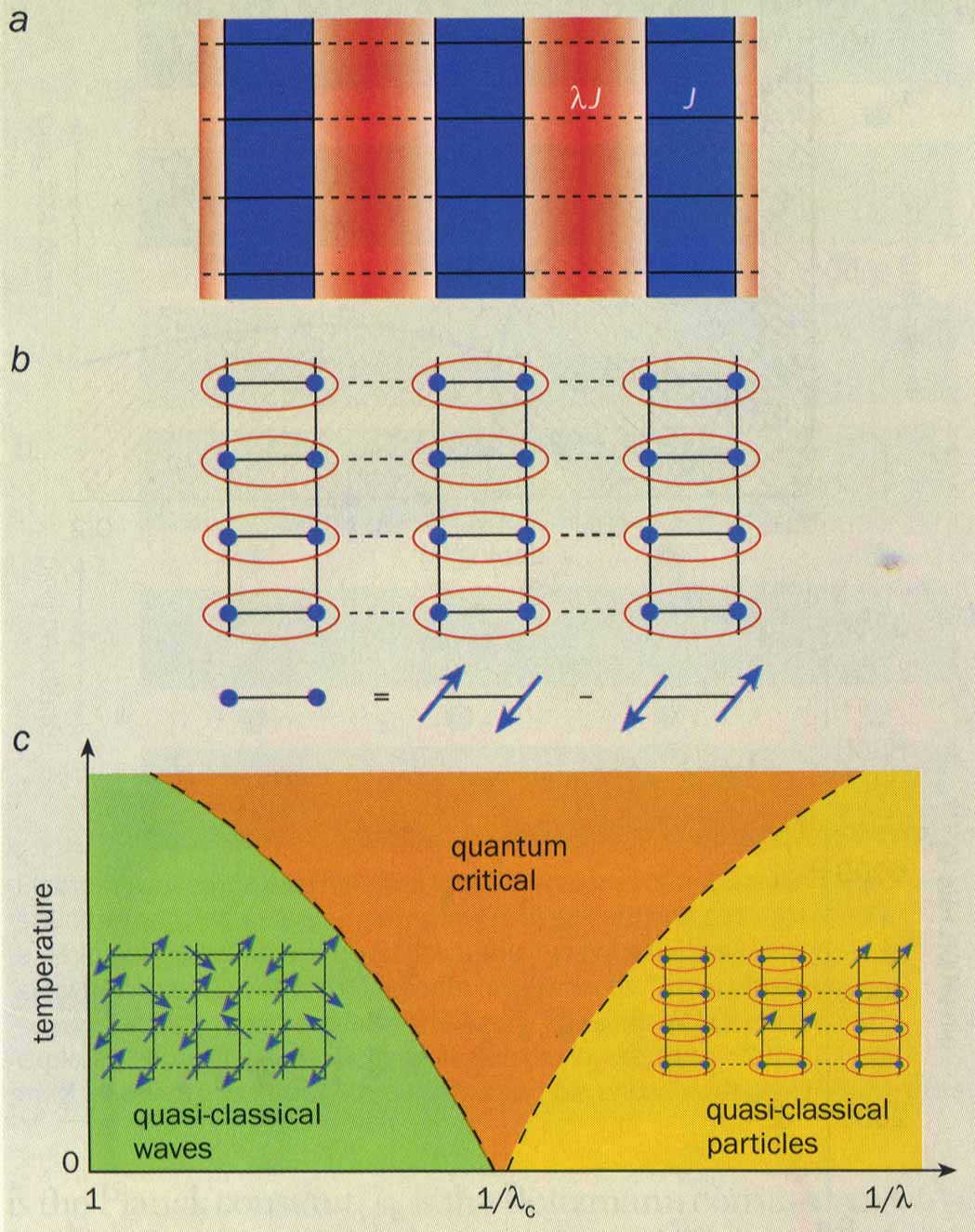
We can construct a simple "toy" model for the destruction of the magnetic order as a function of doping in the presence of these charge-ordered stripes. Imagine that the spins in the hole-poor regions interact with their nearest neighbours by an antiferromagnetic exchange of energy J. Second, the spins at the boundaries of two neighbouring hole-poor regions are coupled by a weaker exchange of magnitude lJ, where l has a value between zero and one [9]. We ignore the spins in the hole-rich stripes and assume that their only role is to mediate the coupling lJ. We have now defined a S = 1/2 antiferromagnet on an anisotropic two-dimensional lattice. In this simple picture the value of l can be changed by altering the amount of strontium in the superconductor. The ground state of this system will evolve as a function of l and, as we shall see, undergo a quantum phase transition at a critical value, l = l_c.

	Figure 3: Stripes in a superconductor
	(a) Segregation of holes in a copper oxide layer into hole-rich stripes (red) and hole-poor regions (blue). Interactions between spins within each hole-poor region (solid line) have an antiferromagnetic exchange energy J. Interactions between spins in neighbouring hole-poor regions (dashed line) have a smaller exchange energy, lJ, where 0 < l < 1 [9]. l can be varied by varying the level of doping. The spins in the hole-rich stripes (not shown) are assumed to only mediate the lJ exchange. (b) For small l, valence bonds (shown in red) form between neighbouring spins. Each bond is a quantum linear superposition of two spin configurations in which the total spin, S, is zero. (c) Phase diagram as a function of temperature and 1/l. The only singularity is at the quantum critical point, l = lc and T = 0. The dashed lines indicate the locations of smooth crossovers. The excitations in the quasi-classical wave regime (green) are spin waves. The excitations in the quasi-classical particle regime (yellow) are broken valence bonds with S = 1. These excitations can hop between sites like particles. No effective classical picture applies in the quantum critical regime (orange).

At l = 1 this model reverts to the ordinary square lattice S = 1/2 antiferromagnet shown in Fig 2a and its ground state exhibits long-range magnetic order. Now consider the ground state for l << 1. Let us assume that each hole-poor region consists of a pair of coupled one-dimensional spin chains. A reasonable trial wavefunction for the ground state is to assume that neighbouring pairs of spins form "valence" bonds in which their orientation is a linear superposition of üp" and "down", such that there is no net magnetic moment on each site (Fig 3b). While this trial wavefunction is not quantitatively correct, it has all the correct qualitative properties, which is currently sufficient. The total spin, S, of this ground state is zero and it is known as a quantum paramagnet. Furthermore, a finite amount of energy (of order J) is required to create an excitation above such a ground state: a valence bond must be broken and the spins point in the same direction to form a S = 1 triplet state.

Since this system has two qualitatively different ground states at small l and l » , there must be a quantum phase transition at some critical value of l or the doping. The properties of this transition have been examined by many theorists - notably Sudip Chakravarty of the University of California at Los Angeles, Andrey Chubukov of the University of Wisconsin, Bertrand Halperin and David Nelson of Harvard University, Matthias Troyer of ETH Zurich, and the author - and now appear to be quite well understood. The phase diagram contains only one thermodynamic singularity, the quantum critical point at l = l_c (Fig 3b). Unlike LiHoF₄ there are no phase transitions at temperatures above absolute zero, although different regions of the phase diagram exhibit distinctly different physical properties.

For l > l_c there is a regime of quasi-classical wave dynamics which we have discussed earlier: the ground state displays antiferromagnetic ordering and the predominant excitations are spin waves. For l < l_c there is a complementary regime of quasi-classical particle dynamics: in the ground state the spins are paired in singlet (S = 0) valence bonds and the excitations are a dilute concentration of triplet (S = 1) states. These excitations can hop from site to site, much like particles, and their de Broglie wavelength is much smaller than the inter-particle spacing, which allows an effective classical description.

In between these two quasi-classical regimes is the fascinating quantum critical regime. The crossover from the quasi-classical particle regime to quantum criticality occurs when the spacing between the particles becomes of order their de Broglie wavelength. Similarly, the crossover from the quasi-classical wave regime to the quantum critical regime happens when short-wavelength spin waves, which cannot be treated classically, proliferate. Neither quasi-classical picture is applicable in the quantum critical regime and more sophisticated theoretical tools are necessary to describe the dynamics.

A key property of the quantum critical regime is that quantum interference effects operate up to a characteristic time, the phase coherence time, which is given by h C/k_B T, where h is the Planck constant, k_B is the Boltzmann constant and C is a universal number that is independent of microscopic details. This remarkable dependence of the phase coherence time on the fundamental constants of nature and nothing else also applies to a number of relaxation rates and transport co-efficients that can be measured in neutron scattering or nuclear magnetic resonance experiments.